HOME > Research Summaries > Determination of Local Fine Structure of Blood Flows by Measurement Coupled Simulation
Research Summaries

Determination of Local Fine Structure of Blood Flows by Measurement Coupled Simulation
Toshiyuki Hayase
Professor
Transdisciplinary Fluid Integration Research Center, Institute of Fluid Science
E-mail:![]()
1. Introduction
Understanding complex blood flows in living bodies is essential to realize advanced diagnosis and treatment for circulatory diseases. The author’s group is doing research to analyze complex blood flows by numerical simulation, experimental measurement, and their coupled method in order to determine the local and fine structure of complex blood flows.
2.Measurement Coupled Simulation of Blood Flows
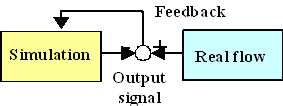
Fig. 1. Numerical realization based on flow observer
In order to make accurate diagnosis for cardiovascular diseases, the method to obtain detailed information of the blood flow is essential. Among a number of measurement methods, an ultrasound color Doppler is widely used since it provides a real-time image of the blood flow non-invasively with a relatively compact equipment. However, the velocity measurement with this apparatus provides only the velocity component along the ultrasound beam, and, therefore, it is difficult to comprehend the three-dimensional blood flow.
As a counterpart of measurement, numerical simulation of blood flows has been studied extensively. Realistic solutions of the blood flows are obtained with real vessel geometries obtained with visualizing methods such as CT or MRI. However, the simulation has inherent problem of difficulties in determining computational conditions such as the vessel geometry, inflow and outflow boundary conditions, and the initial condition. The calculated result of the blood flow is usually similar but not exactly identical to the real one.
In order to overcome these problems, we have proposed numerical realization of the blood flow by integrating the ultrasound measurement and the numerical simulation based on the flow observer [1] (Fig. 1). Since existing theory of observers is not applicable to complex flow problems, design and evaluation of the feedback schemes were made through numerical experiment in simplified 2-dimensional problem [2] or 3-dimensional steady problem.
Fundamentals of the method are given in the followings. Example of ultrasonic measurement integrated (UMI) simulation is shown in Fig. 2. Esophageal ultrasound measurement provides an image as shown in the figure. The configuration of the vessel wall is visualized by B-mode imaging technique. As to the blood velocity measurement, pulse echo technique is used. Doppler shift frequency of the ultrasound beam is converted to the blood velocity.
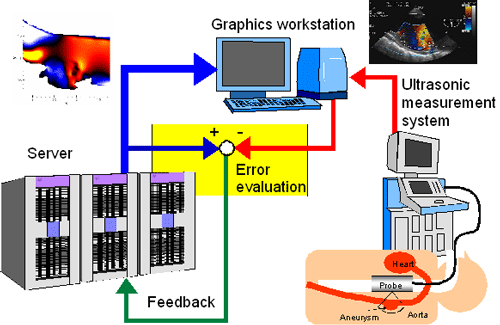
Fig. 2. Prototype of UMI simulation system
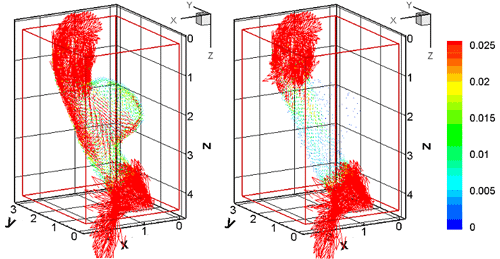
Fig. 3. Velocity error vector in 3D aneurysmal aorta
left:(a) Ordinary simulation right:(b) UMI simulation
In order to construct the flow observer, we first extracted the shape of vessel walls from the ultrasonic image or CT data and then defined a computational domain on an equidistant rectangular computational grid. As the fundamental equations, Navier-Stokes equations and equation of continuity are employed. Discretized representations were obtained by finite volume method and solved by SIMPLER based iterative algorithm. As the boundary condition, a time-dependent parallel flow with a uniform velocity distribution is assumed at the inlet boundary, and a free stream at the exit. Time variation of the flow rate can be estimated from the intensity of the color Doppler signals. The feedback signal is applied in the following procedure. (1) At each time step of the simulation, the difference between measurement and computation for the Doppler velocity is calculated at each monitoring point. (2) Feedback signal proportional to the difference is added to the source term of the Navier Stokes equation and the pressure equation in order to reduce the difference asymptotically.
Since real blood vessels have complex three-dimensional configurations, three-dimensional UMI simulation is essential for practical applications. Fundamental result for the steady flow analysis is shown in Fig. 3 [3]. In the aneurysmal aorta, error velocity vector from the standard solution, which is a model of the real flow, is compared between the ordinary simulation (Fig. 3 (a)) and UMI simulation (Fig. 3(b)). The velocity error is substantially reduced in the UMI simulation in the aneurysm, which is the region of concern and, therefore, defined as the feedback domain.
Measurement integrated simulation was performed for several fundamental flow problems in order to understand basic characteristics of the methodology. Convergence of MI simulation for a fully developed turbulent flow using partial information of the flow was confirmed by a numerical experiment.
In the future study, we are developing an ultrasonic measurement coupled simulation system to analyze the local fine structure of blood flows by integrating an ultrasonic measurement and flow-structure coupled simulation with a super computer system (Fig. 4). Utilizing another measurement device such as MRI or X-ray is also to be investigated.
3. Cellular Flow in Microcirculation
As a fundamental research for modeling of microcirculation, frictional characteristics of blood cells on endothelial cells cultured on a glass plate or a glass plate coated with materials are investigated with an inclined centrifuge microscope.
Leukocytes are concentrated to sites of inflammation by some chemo-attractants. Effect of the neutrophil plugging of a capillary on the blood flow is investigated both numerically and experimentally together with the deformation of the cell in passing through the capillary(3).

(a) Ultrasonic measurement system

(b) Super computer system in Advanced Fluid Information Research Center
Fig. 4. Ultrasonic measurement coupled simulation system
4. Conclusions
The author’s group is doing research to analyze complex blood flows by numerical simulation, experimental measurement, and their coupled method. The coupled method enables us to perform a highly accurate and high speed analysis of the local and fine structure of complex blood flows.
References
[1] Hayase T and Hayashi S. State Estimator of Flow as an Integrated Computational Method with the Feedback of Online Experimental Measurement. Journal of Fluids Engineering. Transactions of ASME 119, 814-822, 1997.
[2] Fumamoto K, Hayase T, Shirai A, Saijo Y, and Yambe T. Fundamental Study of Ultrasonic-Measurement-Integrated Simulation of Real Blood Flow in the Aorta. Annals of Biomedical Engineering 33, 413-426, 2005.
[3] Shirai A, Fujita R, and Hayase T. Simulation Model for Flow of Neutrophils in Pulmonary Capillary Network. Technology and Health Care 13-4, 301-311, 2005.