HOME > Research Summaries > Multi-scale Blood Flow Analysis for Human Circulation System
Research Summaries

Multi-scale Blood Flow Analysis for Human Circulation System
Takami Yamaguchi* and Takuji Ishikawa
Professor
Department of Biomedical Engineering, Graduate School of Biomedical Engineering
E-mail:![]()
Abstract
We have been investigating the cardiovascular system over micro to macro levels by using conjugated computational mechanics analyzing fluid and solid interactions. In this article, we introduce our recent researches on ATP transport in a cerebral artery with aneurysm, the progress of cerebral aneurysm due to mal-adaptation of arterial wall, the blood flow considering more than 16 thousands of red blood cells' motion, and platelets aggregation in blood flow.
1. Introduction
Human cardiovascular system is always under the integrated nervous and humoral control of the whole body, i.e., in homeostasis. Multiple feedback mechanisms with mutual interactions among systems, organs, and even tissues provide integrated control of the entire body. These control mechanisms have different spatial coverages, from the micro- to macroscale, and different time constants, from nanoseconds to decades. We think that these variation in spatial as well as temporal scales should be taken into account in discussing phenomena in the cardiovascular system.
In this background, we have been investigating the cardiovascular system over micro to macro levels by using conjugated computational mechanics analyzing fluid and solid interactions. In this article, we introduce our recent researches on ATP transport in a cerebral artery with aneurysm, the progress of cerebral aneurysm due to adaptation of arterial wall, the blood flow considering more than 16 thousands of red blood cells' motion, and platelets aggregation in blood flow.
2. Computational Biomechanics for Human Circulation System
2.1. ATP transport in a cerebral artery with aneurysm
ATP has been shown to be an important modulator of vascular conditions. ATP can alter the arterial diameter by controlling the production of NO etc. On the endothelial surface, the ATP transferred from flowing blood undergoes hydrolysis by an enzyme as follows: ATP to ADP through AMP, and finally to adenosine. We focused on this phenomena, and the ATP concentration on endothelial cells (ECs) of aneurysms is investigated by using numerical analysis (see Fig. 1). The results show that the ATP concentration is strongly affected by the configuration of parent artery relative to the aneurysm.
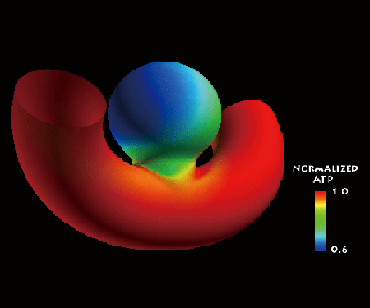
Fig. 1. Distribution of ATP concentration around an aneurysm occurs at a vent artery
2.2. Progress of cerebral aneurysm
The purpose of this study is to develop a numerical model that can be used to analyze the growth of aneurysm. We take an adaptive response of the arterial wall into consideration, assuming that artery luminal area is increased locally where the wall shear stress due to blood flow is much higher. We propose a mathematical model to express the adaptive response of the arterial wall and consequent changes of the arterial shape. As a result of applying the model to a U-shaped artery model with a slight twist, a mechanically stable shape of the aneurysm is obtained as shown in Fig. 2.

Fig. 2. Simulation of the progression of a cerebral aneurysm due to wall shear stress oscillation
2.3. Blood flow in a small artery and deformation of red blood cells
The collective behavior of blood under the influence of the mechanical interactions between RBCs is essential in determining the rheological properties of blood as a mass. We have proposed the cell flow model (1), a type of Eulerian-Lagrangian model from the standpoint of multiscale mechanics and based on the minimum energy principle. Assuming that the macroscopic flow field is not affected by the motion of individual RBCs, i.e., one-way coupling, motions of RBCs are calculated from the macroscopic flow field by theoretical / numerical analysis. This method is suitable for a vector / parallel computer system such as the Earth Simulator system, because the solving method consists of explicit procedures. Figure 3 shows the results obtained in this study, in which the motion of up to 16 thousands of RBCs are computed.

Fig. 3. Motion of a large number of red blood cells in a small artery
2.4. Flow of malaria infected blood
Malaria-infected red blood cells (IRBCs) show various changes of mechanical properties. IRBCs lose their deformability and develop the properties of cytoadherent and rosetting. To clarify how these changes advance microvascular occlusion, we need qualitative and quantitative information on hemodynamics in malaria infection, including the interaction between IRBC, healthy RBCs, and endothelial cells. We developed a numerical model of blood flow with IRBCs based on conservation laws of fluid. The deformability and adhesive property of IRBCs were simply modeled using springs governed by Hook’s law. Our model could express basic behavior of IRBC, including rolling motion due to cytoadhesive interaction with endothelial cells and complex interaction with healthy RBCs (Fig. 4). We confirmed that such interactions significantly increase the flow resistance, particularly when knobs were developed on the IRBC membrane.

Fig. 4. Malaria infected blood flow in microcirculation simulated by a particle method
3. Conclusion
In this article, we introduced our recent researches on the cardiovascular system over micro to macro levels by using conjugated computational mechanics analyzing fluid and solid interactions. In considering clinical applications, however, one needs to consider more about biological complexities in the analysis of blood flow, especially with respect to disease processes. A disease is not just a failure of machine. It is an outcome of complex interactions among multi-layered systems and subsystems. We expect that biological phenomena, including disease processes, will be clarified in the future by integrating new understandings of macroscale and microscale hemodynamics, if we continue to be together with advances of related sciences and technologies.
References
[1] Wada S and Kobayashi R. Numerical simulation of various shape changes of a swollen red blood cell by decrease of its volume. Trans Japan Soc Mech Eng A 69, 14-21, 2003.
[2] Kamada H, et al. Computer simulation of formation and collapse of primary thrombus due to platelet aggregation using particle method. Trans Japan Soc Mech Eng B 72, 1109-1115, 2006.